逆向物流流量和需求不确定性下闭环供应链规划的鲁棒优化模型外文翻译资料

英语原文共 15 页，剩余内容已隐藏，支付完成后下载完整资料

逆向物流流量和需求不确定性下闭环供应链规划的鲁棒优化模型

关键词：

鲁棒优化；闭环供应链；再生材料；逆流不确定性；需求不确定性；

摘要：

人们对环境污染的认识、对回收的兴趣以及闭环供应链管理的重要性都在不断提高。在闭环供应链中，生产计划不仅受客户需求不确定性的影响，还受收藏家对逆向物流方面困难的影响。因此，开发一个鲁棒的闭环供应链模型来响应逆向物流的不确定性是十分重要的。在本研究中，我们发展一个确定性的混合整数优化模型和稳健的对应方以应对回收产品和时尚企业的客户需求不确定性。我们证明了一个具有不确定性预算的鲁棒对手等价于 在特殊条件下具有箱型不确定性的鲁棒对手。为了避免保守主义鲁棒解，一个替代优化问题被发展成为利用预算不确定性的问题。为了验证该模型的性能，本研究进行了数值实验。 仿真结果表明，该模型对不确定性有很强的响应能力，且优于确定性模型和其他鲁棒模型。

1. 介绍

供应链管理是指对一系列过程例如采购原材料、生产成品和产品交付给消费者的管理，。随着产品多样化，供应商、制造商和分销商的数量增加，供应链管理变得越来越重要。。目前，客户不仅想购买低价多样的产品，也还希望企业在整个供应链过程中成为一个环保型企业。超越生产高品质的产品并以低价出售，环保型公司友好形象已成为顾客挑选产品的企业新标准（Niinimaeuro;ki and Hassi, 2011）。因此，公司需要付出额外的努力去成为生态友好型企业并保持可持续发展进程。设计和运行一个闭环供应链是可持续发展的一个最重要问题。此外，鉴于生产者责任延伸政策，回收和回收客户的报废产品是公司重要任务。

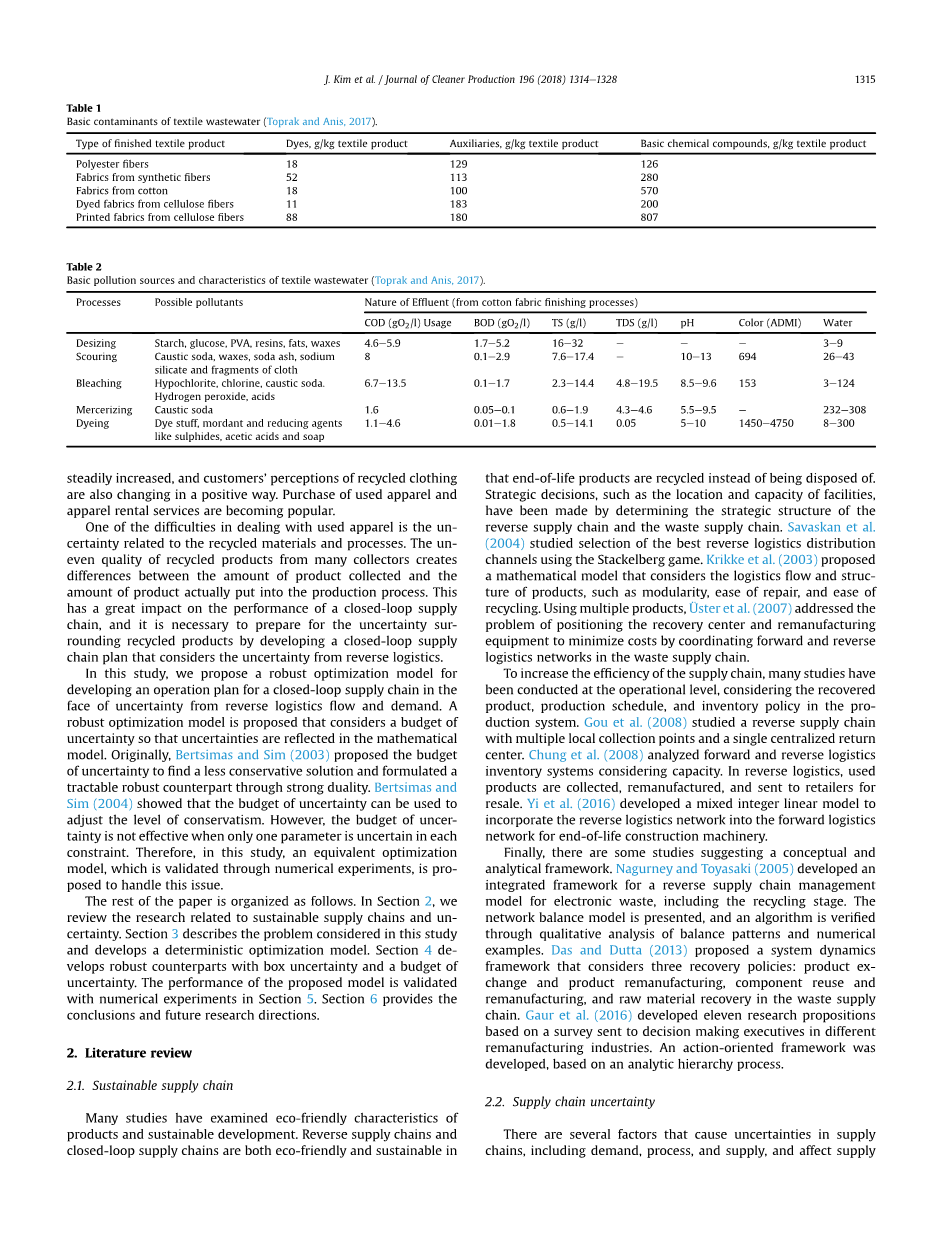
服装和纺织业是产生大量污染物的密集型产业之一（Yin et al., 2016）。除了生产过程所产生的污染物，焚化、使用服装垃圾填埋也严重的环境退化（Hustvedt and Dickson, 2009）。 最近，快时尚产业因在短时间内连续生产多种产品并以低价供应，已经越来越受欢迎。这些短生命周期产品会导致大量的服装浪费，从而导致更快的污染扩散。工业界正在使用各种化学物品生产纺织品，特别是在印染过程中（Kant, 2012）。酸性和碱性化合物是最常见的 无机污染物，它们的化学成分以及在水中的生化相互作用不同。有些污染物是 可生物降解，但会降低水质并影响海洋生物的生存，如表1和表2所示。然而， 二手服装只需要简单的清洗和修理，所以它不会造成环境问题，而且客户也可以购买或租赁 价格低廉的独特产品。尽管有这些优势，二手服装市场规模仍然很小，服务仍未完全组织起来。二手服装市场和租赁服务不能成为解决时尚产业环境问题的基本解（Goworek et al., 2012）。最近，人们对回收衣物的兴趣稳步增加，顾客对回收衣物的看法也在以积极的方式改变。购买二手服装以及服装租赁服务正变得流行起来。

表1纺织废水中基本包含物：

表2：纺织废水的基本污染源和特征(Toprak和Anis. 2017)。

处理二手服装的难点之一是与回收材料与回收过程的不确定性。从许多收集者手中回收的产品的不均匀质量造成了收集的产品数量与实际投入生产过程的产品数量并不相同。这个 对闭环供应链的表现有很大影响，并且有必要通过逆向物流不确定性的闭环供应链计划为回收产品的不确定性做好准备。

在这项研究中，我们提出了一个鲁棒优化模型来为面对来自逆向物流和需求的不确定性的闭环供应链制定运营计划。鲁棒优化模型提出了考虑不确定性预算使得不确定性反映在数学上的不确定性。最初，Bertsimas and Sim（2003）提出了不确定性预算来找到一个不太保守的解，并制定了一个通过强二元性的易处理的健壮对应物。Bertsimas and Sim (2004)表明不确定性预算可以用于调整保守主义的水平。然而，当每个限定条件中只有一个参数是不确定的时，不确定性预算是无效的。因此，在本研究中，通过模型经数值实验验证了的等效优化模型被提出用于处理此问题。

论文的其余部分安排如下。在第2部分中，我们回顾与可持续供应链和不确定性供应链相关的研究。第3部分描述了本研究中考虑的问题并建立了确定性优化模型。第4部分- 研究具有盒不确定性和预算不确定性的鲁棒优化模型。第5部分用实验数据来验证此模型的性能。第6节提供结论与未来研究方向。

2、文献综述

2.1可持续供应链

许多研究已经验证了产品和可持续发展的环保型特点。逆向供应链和闭环供应链既环保又可持续，因为报废产品被回收利用而不是被处理掉。战略决策，如场所、设施的容量，都是通过逆向供应链与废物供应链的战略结构来确定的。Savaskan等人（2004)使用Stackelberg游戏来研究最佳逆向物流配送的选择。Krikke et al. (2003)提议考虑物流流动和产品结构的数学模型，例如模块化、易修复性和易回收。通过使用多种产品，Uuml;ster et al. (2007)讲解了关于回收中心定位和再制造设备通过向前协调设备以及废物供应链中的逆向物流网络来使成本最小化的问题。

为了提高供应链的效率，考虑了回收产品、生产计划和生产系统的库存策略，许多研究已经在运行层面进行。Gou 等人(2008)研究了具有多个本地收集点和一个集中返回中心的逆向供应链。Chung 等人（2008)分析考虑容量的正向和逆向物流的库存系统。在逆向物流中，旧产品被收集、再制造并发送给零售商再销售。Yi et al. (2016)为报废工程机械开发了一个将逆向物流网络融入正向物流网络的混合整数线性模型。

最后，有一些研究提出了一个概念和分析框架。Nagurney 和Toyasaki（2005）开发了 电子废弃物模型的逆向供应链管理的集成框架，包括回收阶段。网络平衡模型被提出，并对此算法通过平衡模式的定性分析和数值计算例子进行了验证。Das and Dutta（2013）提出了考虑三种恢复策略的系统动力学框架：产品交换和产品再制造、部件再利用与 再制造和废物供应链中的原材料回收。Gaur等人2016)提出11个基于一项调查对象是再制造工业的研究命题，建立了一个基于层次分析法的面向行动的框架。

2．2供应链不确定性

有几个因素会导致供应链的不确定性，包括需求、过程和供应，以及供应链计划、调度和控制。第一，需求不确定性在文献中被广泛考虑。例如，Gupta and Maranas (2003)考虑了供应链过程中的需求不确定性。Tsiakis 等人(2001)讨论了为解决不确定性需求的多个仓库和配送中心的数量、位置和大小的决策问题。Bernstein and Federgruen (2005)重点在于鉴别零售商响应分布式供应链中不确定性需求的竞争性行为。第二，有关于供应链过程不确定性的研究。Peidro et al. (2009)引入了考虑需求和过程不确定性的模糊数学模型。Petrovic et al. (1998)提出了一个模糊仿真模型来开发决策支持系统以应对设施不确定性。第三，关于供应不确定性，Tomlin（2006）从两个不同的供应商角度提出了供应链规划；一 在供应不确定的情况下以低的成本供应；另一个则在不存在供应不确定性的情况下以更高的成本供应，。Li 等人(2010) 建立了一个协调机制来使供应者利益最大化。Li等人(2010)通过考虑两个供应商向一个零售商供货的不确定性，推导出一个均衡，建立了一个协调机制，使两个供应商的利润最大化。对于闭环供应链，除了需求、流程和供应不确定性，考虑退货产品的逆向物流不确定性也很重要。Amin 和Zhang提出了一个混合整数线性规划模型去解决以基于产品需求与退货产品不确定性随机模型为情景的闭环供应链的设计问题 。Ramezani等人。（2013）呈现随机多目标优化模型去解决正向及逆向物流的不确定性问题。

处理供应链不确定性的数学方法可以分为模糊的、随机的以及稳健的三种优化方法 。Vahdani等人（2013）通过数学推导出考虑正向和逆向物流的基于模糊优化的集成模型。使用模糊优化Oeuro;zceylan和Paksoy（2014）提出了一个模型，其中包括防止产生次优解的战略及战术决策。Talaei等人（2016）为需求不确定性下的多产品闭环供应链提出了基于编程的模糊稳健选址模型以及分配模型 。

也有研究使用随机优化来处理供应链中的不确定性。Kenne等人（2012）考虑到设备故障和修理的不确定性，确定了闭环供应链的逆向物流。Amin 和Zhang（2013）提出了基于情景的混合整数规划模型来解决闭环供应链中产品需求和回收率不确定性问题。Zeballos等人（2014）使用场景来呈现考虑原材料供需不确定性的多产品闭环供应链的设计与规划模型。

稳健优化方法也用来处理不确定性问题。Hatefi和Jolai（2014）开发了一个稳健可靠模型用来解决参数不确定性和设施中断环境下正向逆向物流网络设计问题。Gao和 Ryan（2014）提出了一种针对多周期闭环供应链网络设计问题的混合模型来考虑两种管制政策的连锁网络设计问题，并推导出盒形和椭球形不确定性集下的可处理的鲁棒副本。Keyvanshokooh等人（2016）提出了一项应用稳健优化与随机优化的闭环供应链的利益最大化模型。

2.3 鲁棒优化

通过对供应链不确定性的回顾，我们发现参数的变化会导致供应链的不确定性。尽管 模糊、随机和概率优化处理参数不确定性，但每种方法都是以不同的方式来考虑不确定性。相较于其他方法，模糊理论更侧重于定义不确定性参数。它提议使用隶属函数来定义现实的模糊性。随机和概率方法假设不确定参数的概率分布是已知的。一些研究通过预先定义不确定场景及其概率来处理不确定性。本文所使用的稳健优化方法定义了一个不确定性集并对最坏的情况进行处理，以保证在不确定集内实现的不确定解的可行性。然而，基于最坏情况的方法可能会产生一些稳健的优化方法试图避免的保守解。 Mulvey等人(1995)考虑了不确定情景，将变量分为两类:设计变量和控制变量。设计变量在不确定性实现之前确定，控制变量在不确定性实现之后确定。Soyster(1973)首次提出了基于集合的不确定性的概念，而不是通过情景来定义不确定性。不失一般性的优化问题可表示为：

min cx (1)

s:t: Ax≦b (2)

在公式（1）和（2）中，x是一组决策变量，A, b, c是系数。式（2）进一步细分表示第i个约束条件为sum;a_ijx_j ≦b_i..。

一个不确定的参数atilde;可以定义与j一个额定值,通常设置为E atilde;变量，其对实际参数实现的贡献为由随机变量xi;与正常数acirc;之积决定:

（3）

根据atilde;的定义，不确定参数线性参与约束或目标函数的模型可以表示为:

（4）

定义为第i个约束的第j个系数的集合并假设参数的不确定性对应是对j的反映。将施加于模型上的不确定集定义为Uij，允许将式(4)的鲁棒对应式表示为式(6)。将x的整个不确定集施加于模型上，保证了不确定集中所有不确定实现的最优解的可行性。

当表示施加于约束上的不确定性集的内部最大化部分被封闭形式的解或有限数量的方程所取代时，鲁棒对应项即成为确定性的。Ben-Tal和Nemirovski(1999)考虑了基于集合的不确定性而不是不确定性场景，并定义了一个椭球面不确定性集合来避免盒型不确定性集中最坏的情况。Bertsimas和Sim(2004)通过定义不确定性预算解决了保守性问题，允许决策者调整可实现的最大不确定性。预算的不确定性，Gamma;i对所有的约束条件i的取值在【0，|Ji|】范围内，且可以用来调整参数不确定性。基于Gamma;i，鲁棒解通过反映参数变化在（Gamma;i-Gamma;j）范围内的不确定性水平|Ji|来确定的。数学模型如下列式（8）和式（9）所示：

第二项的方程(9)被定义为，其决策变量为；使用给定的和,它可以制定以下线性优化问题:

最后,被对偶问题和对偶变量pij所代替，推导出考虑不确定性预算的可控制鲁棒模型如下:

3.问题描述和确定性模型

在闭环供应链中，有五种类型的生产恢复选项，包括修理，翻新，维修生产，同类相食，和循环利用(Thierry et al.， 1995)。根据行业不同，可以选择不同类型的恢复选项并设计一个合适的闭环供应链。例如，轻微损坏产品的修复选项被广泛用于耐用商品。翻新选项用于某些产品中的模块被修理或是被替代的情况。翻新的玻璃纸电话和家用电器就是很好的例子。电子工业的回收利用利用内部核心部件生产新产品，其余的产品被处理，因此，电子产品的回收利用取决于核心部件的性能。Krikke等人(2003)提出了冰箱行业的闭环供应链，Kannan等人(2010)提出了电池回收的供应链模型。时装业使用收集到的最终使用产品的所有可用部分，而放弃其他部分。由于这些特性，使用过的产品可以根据它们的条件被部署到一系列连续的过程中。因此，时装业可以考虑维修、再制造和回收利用等选择(Oh and Jeong, 2014)。

在本研究中，我们考虑一个包含原材料供应商、制造商和客户的三级时装供应链。制造商使用纱线、织物和服装制造工艺生产服

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[234121]，资料为PDF文档或Word文档，PDF文档可免费转换为Word