外力驱动聚合物链吸附与构象的计算机模拟研究

摘要：本文采用蒙特卡罗模拟方法研究了柔性聚合物链在平行于吸引平面的外力F作用下的临界吸附行为。临界吸附温度随F的增加线性下降,

表明驱动力抑制聚合物的吸附。聚合物的构象也受驱动力的影响。然而，F的影响取决于驱动力和温度之间的竞争。在强力或低温下,

聚合物沿着力的方向被拉伸，而在弱力或高温下，聚合物不被拉伸。当力与温度相当时，聚合物可能被拉伸成垂直于驱动力的形状，在以下， 我们观察到由平行到垂直的构象转变，并且通过降低温度再次到平行。我们发现垂直拉伸的构象使得聚合物链沿着驱动力的方向同步移动。此外，构象转变归因于驱动力和温度之间的竞争和合作。

关键词：临界吸附; 聚合物; 驱动力; 构象; 蒙特卡罗模拟

引言

聚合物链的吸附在胶体稳定性、表面涂层、生物相容性、润湿性、液相色谱和毛细管电泳等方面都有重要应用^[1-5]。这些应用通常涉及系留聚合物的剪切。尽管目前的应用非常广泛，但是剪切聚合物链的非平衡动力学知之甚少。实验研究主要集中在测量流变特性或聚合物溶液中光或中子的散射^[6]。由于聚合物在剪切作用下的微观动力学没有直接观察，因此模拟对于预测聚合物在剪切流动中的分子动力学具有重要意义^[7]。模拟和数值计算主要集中在平均链性质上^[8-11]。稀释聚合物溶液的流动显示出一些有趣的宏观效应，包括粘度，增强的法向应力和湍流减阻^[12]。这种非牛顿流体性质有助于通过剪切改变聚合物构象^[7,13,14]。也被发现聚合物结构的变化与剪切力直接相关^[7]。

聚合物链在固体表面的吸附已经被广泛地研究了理论^[15,16]， 数值^[17-20]，和实验方法^[21,22]。最近，研究驱动力对端接聚合物的影响是相当有趣的^[23-26]。施加到聚合物上的外部驱动力可以影响聚合物链的吸附行为以及构象性质^[24-26]。在吸附-解吸相图中，二阶相变(热解吸)和一阶相变(机械解吸)的临界力随温度低于临界吸附温度而变化^[26]。聚合物保持在临界力以下吸附，并在临界力以上解吸。在不同的吸附强度和驱动力值下，聚合物在相图中的典型构象分别表现为各向同性相、拉伸相和吸附相。将聚合物垂直于表面的一端拉伸通常可以减少聚合物的吸附，而平行于表面的拉伸则可以促进聚合物的吸附^[27]。在模拟侧向力对聚合物一端的影响时，在原子力显微镜拉伸实验中，力使聚合物沿垂直于外力方向变平^[28]。此外，剪切流对聚合物的吸附。对于自由柔性聚合物，表面接触数量随着剪切强度的增加而减少，直到发生完全解吸为止^[29] ；而对于端系聚合物，表面吸引力降低了聚合物的拉伸，而剪切流动增强了聚合物的吸附^[30]。然而，表面平行驱动力(或流动)下聚合物吸附的机制尚不清楚。上述研究启发我们探索外部驱动力对聚合物吸附和构象性质的影响。

由于高粘度，聚合物的运动主要是以层流的形式^[31]。固体表面对流动产生摩擦阻力，导致表面附近的剪切场。Couette剪切流动沿垂直于表面的方向具有均匀的剪切应力和速度梯度^[31]。 Oldroyd-B模型在本构方程中分离了剪切流动的活化和速度两个方面，这有助于理解各种复杂流体在剪切场中的非新流体行为。因此，有必要在分子水平上了解聚合物在剪切流动中的变形。除了实验和理论之外，分子模拟已经成为研究聚合物剪切流动的重要工具^[12,33]。蜗杆状链(WLC)模型适用于描述具有特征弯曲能量的聚合物从柔性到刚性棒的构象特性^[34]。自由连接链(FJC)模型适合于理解柔性聚合物链^[35]。聚合物流体假设移动粒子的动量立即受到局部热涨落的阻尼。本文采用蒙特卡罗(MC)模拟方法^[31]，在无速度梯度的情况下，采用均匀驱动力模拟库埃特剪切流。该模拟相当于将电场平行于所有单体都受到恒定外力，这与剪切流不同。此外，吸附的聚合物相对较薄，因此剪切力可以被认为是表面上吸附的聚合物的近似常数。

本研究旨在全面了解系留聚合物在平行于吸引面的均匀驱动力作用下的吸附和构象特性。本文的结构如下组织。在第二部分，我们介绍了仿真模型和计算方法。在第三部分，我们讨论在驱动力作用下聚合物的吸附和构象的结果。最后，我们在最后一节总结了我们的主要结果。

仿真模型与计算方法

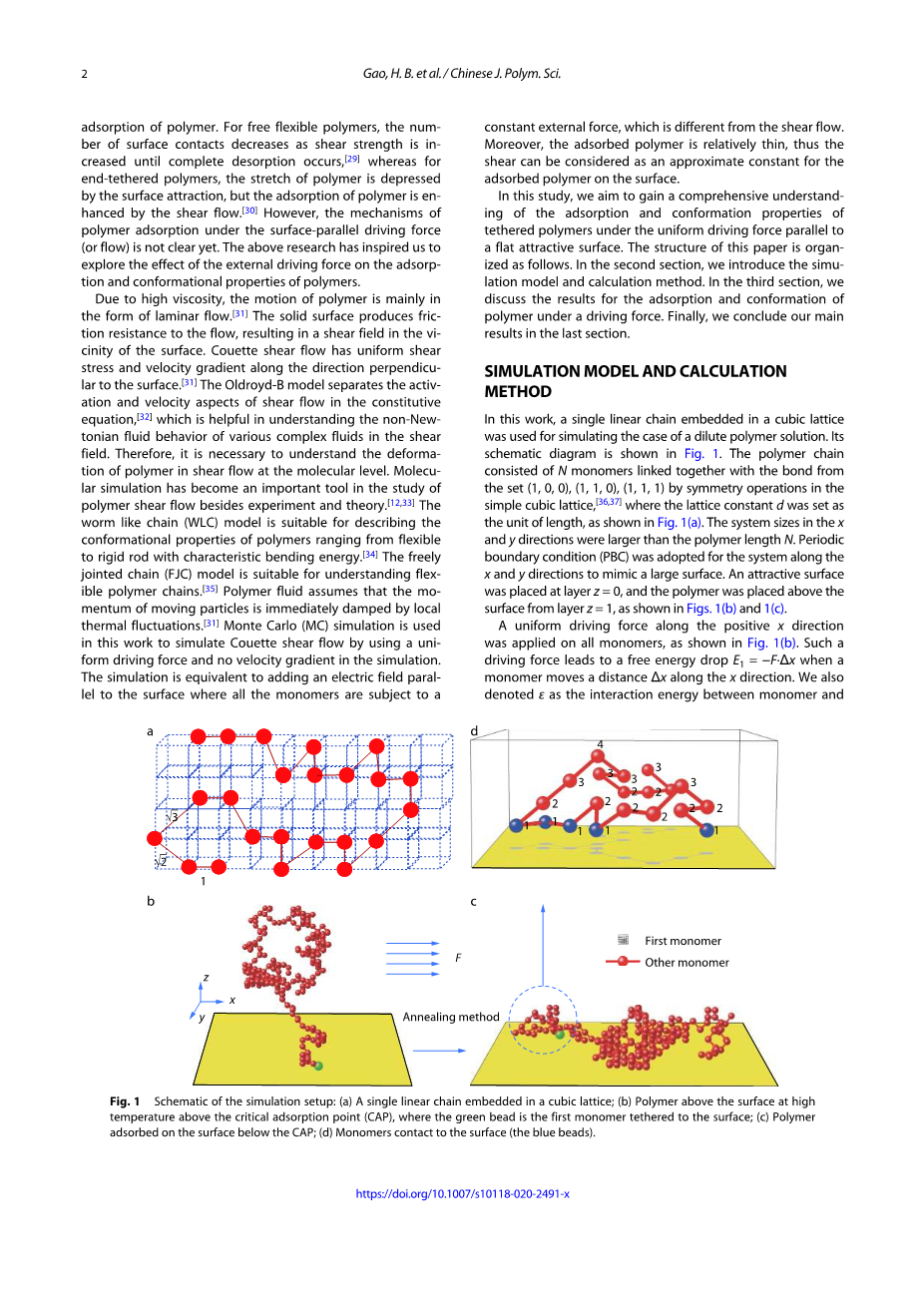
在这项工作中，一条嵌入在立方晶格中的线性链被用来模拟稀释聚合物溶液的情况。它的示意图如图 1 所示。聚合物链由 n 个单体组成， 它们通过简单的立方晶格^[36,37] 中的对称运算与集合(1,0,0) ，(1,1,0) ，(1,1,1)中的键连接在一起，其中晶格常数 d 被设定为长度单位，如图1(a)所示。系统在 x 和 y 方向的尺寸大于聚合物长度 n 。对于沿 x 和 y 方向的系统，采用周期边界条件(PBC)来模拟大的表面。如图1(b)和1(c)所示，在 z = 0 层放置一个有吸引力的表面，聚合物从 z = 1 层放置在表面上方。

如图 1(b)所示，沿着正 x 方向的均匀驱动力施加在所有单体上。当单体沿 x 方向移动距离 x 时，这样的驱动力导致自由能降 。我们也将表示为单体与表面接触时，即单体位于 z = 1 层时，单体与表面之间的相互作用能，如图1(d).所示在 z = 1 层上的单体提供了表面接触。聚合物的接触能是 ，M表示表面接触的数目。在模拟中， 被设定为温度单位， 为波兹曼常数。虽然任何两个非键合单体之间的相互作用是自我避免的，键交叉是允许的，导致高流动性的聚合物链在模拟。

图1 模拟装置示意图: (a)嵌入立方晶格中的单个线性链; (b)在临界吸附点(CAP)以上的高温高于表面的聚合物，其中绿色珠子是第一个与表面连接的单体; (c)在 CAP 以下的表面吸附的聚合物; (d)单体与表面接触(蓝色珠子)。

在模拟的开始阶段，使用 Rosenbluth-Rosenbluth 方法生成了端系聚合物链^[38] ，第一个单体位于与表面接触的位置(0,0,1)。第一个单体被限制在第一层。为了研究表面上聚合物的动力学，允许第一单体在第一层上移动，如图1(b)所示。由于热涨落和外部驱动力，聚合物链经历了一系列移动。一个单体被捡起并试图移动到六个最近的邻居中的一个，不包括第一层上的第一个单体。如果同时满足以下四个条件，即: (1)新位点位于表面以上(z gt; 0) ; (2)满足自回避条件(任何晶格位点只能由一个单体占据) ;(3)所有的键向量都在键长{1，，}，(4)根据exp实现玻尔兹曼因子，其中是由于移动引起的能量位移，0lt;Plt;1。对于单体的移动，能量转移可以表示为，其中, 。对于能量的增加、不变性和减少，和的值可以分别取为1、0和minus;1。参数依赖于运动的方向，而依赖于吸附和解吸的行为。因此，在MC模拟中，接受运动的概率依赖于F和T，聚合物的性质也依赖于F和T。在一个MC步骤(MCS)中，聚合物链中的所有单体平均尝试移动一次。

(1)

我们采用MC模拟退火方法^[19]，通过将温度从T=8降低到T=0.05来研究聚合物的性能。在临界吸附点(CAP)附近选择温度步长Delta;T=0.05，在远离CAP附近采用稍大的Delta;T值。在之前的温度下的最终配置被用作当前温度的初始配置。在每个T上，我们使用约来平衡聚合物^[37,39]。然后，以0.1tau;MCS的时间间隔记录聚合物对下一个100tau;MCS的构象。在模拟中，实现了超过1000个独立的运行，然后结果平均超过106个独立的配置。

结果及讨论

为了清除的表示不同驱动力 F 和温度 T 值下聚合物链的构象。图2显示了构象的二维(2D)投影的草图。圆圈或椭圆形圆圈表示聚合物在表面上的投影，包括其大小和方向。圆表示它的投影在各个方向上都是均匀的，而椭圆表示它的投影方向是各向异性的。圆形投影取决于温度，几乎与驱动力 F 无关。椭圆投影的大小和方向取决于驱动力 F和温度 T 。在图2中，破折号曲线是影响聚合物投影取向的临界力。当 时，驱动力对聚合物的取向没有影响，否则它将使聚合物变形。固体曲线 是使投影的长轴方向与驱动力 F 的方向一致的临界力。当 时，聚合物将沿着驱动力 F 的方向延伸。当时，聚合物的构象取决于 F 和 T。分离吸附聚合物和解吸聚合物的 CAP 随着驱动力 F 的增加而减少。驱动力 F 对解吸和吸附构象尺寸和取向的影响主要分为三个主要区域: 强驱动力时的力主导区(FD)、弱驱动力时的温度主导区(TD)和驱动力时的力-温度竞争协同区(FTCC)。

图2 不同温度 T 下不同驱动力强度 F 作用下聚合物表面构象的二维投影示意图。圆圈或椭圆形圆圈表示投影的大小和方向，其中力 F 的方向是水平向右的。阐述了三个主要区域: 固体曲线 上的力主导(FD)区域、破折号曲线下的温度主导(TD)区域和与 之间的力-温度竞争-合作(FTCC)区域。是聚合物的临界吸附温度(CAP) ，左边是吸附状态，右边是解吸状态。

在 TD 区域，聚合物的投影在所有方向上都是均匀的，并且投影面积随着温度的降低而增加。在 FD 区域中，由于驱动力，聚合物被拉伸成不对称的轮廓。聚合物的投影为椭圆形，其长轴方向与外力方向相同聚合物拉伸的增加。这种现象之前已经在溶液中的聚合物中观察到。然而，在 FTCC 区域，随着温度的降低，聚合物的取向经历了如下四个不同的温度区域。在高温下，聚合物的投影也是均匀的。在 CAP 附近，聚合物的投影沿着力方向略微拉伸。在低于 CAP 的温度下，聚合物的投影沿着与驱动力垂直的方向略微拉伸。然而，在接近零的温度下，聚合物的投影也沿着驱动力方向拉伸。在与吸引表面平行的驱动力作用下，聚合物 的吸附和构象特性的细节描述如下。

聚合物的临界吸附

我们研究了在驱动力作用下聚合物链对表面的吸附行为。我们计算了表面接触的平均分数，其中是表面接触的平均数量。分数可以看作是吸附程度的顺序参数。通过分析有限长聚合物在不同温度下的行为，可以确定无限长聚合物的CAP^[41]。聚合物的CAP预计将由有限尺度尺度理论确定。在CAP附近，可以表示为^[42]：

(2)

其中ϕ为交叉指数，为比例温度，为EKB中所采用的临界指数^[43]。在等式中的第二项,当从 退火到 时会改变符号。

图3(a)显示了在弱驱动力F=0.1附近的不同温度下，对N的依赖关系。从图中可以看出，-N曲线在低温下略微向上凹，在高温下向下凸。同时，显示的最佳幂律行为，可以表示为^[43]：

(3)

图3 在从T=1.35到T=1.80的温度下，不同驱动力值(a)F=0.1和(b)F=1.0的与N的对数-对数图。链长从N=40到N=400不等。对于=1.67，F=0.1(a).的最佳斜率的平均值。

因此，表征聚合物吸附转变的和ϕ，可以通过使用等式搜索最佳匹配的幂律行为来估计(3).通过模拟数据的插值处理，得到了附近其他温度下的值，在F=0.1时发现了无限长聚合物的=1.67和=0.52。我们用相同的方法在F=0（不包括）处得到了几乎相同的值和ϕ值。我们的结果与没有驱动力的末端接枝聚合物的结果大致相同^[41]。在TD区域，由于弱驱动力和主导温度，可以用有限尺寸尺度法估计CAP()。然而，在FTCC和FD区域，由于外部驱动力和温度的共同作用，不能通过有限尺寸的尺度法确定，因为没有一个温度值满足等式中的函数（3），如图3中F=1.0的(b)所示。在F=1.0时，我们只找到向下的凸曲线。

在讨论聚合物的吸附和构象的背景下，有限的链长也是相当有趣的。下面，我们以链长N=200为例，其他大链的结果也表现出类似的定性行为。此外，还根据能量波动估算了。能量波动，类似于热容，可以为吸附转变提供有用的信息^[44]。过渡点可以由接触能量波动中最大值的位置确定，表示为为了。对于有限的链长，波动的峰值对应于临界吸附温度(F）^[18,31]。对N=200和不同驱动力值F=0、0.3、0.5、0、8、1和1.2的结果如图4所示。(F)的估计值如图4所示。可以清楚地看出，(F)随着外部驱动力F的增加而几乎呈线性下降。

图4 不同温度下的接触波动。插图显示了N=200的过渡点对驱动力的依赖性。

在不同的驱动力F=0、0.5和1.0以及链长N=200条件下，表面接触的平均分数与温度T的依赖关系如图5所示。值在高温下为0到接近于零的温度下为1。在中间温度下，随温度T的降低而单调增加。然而，有两个中间温度区域。在一个区域，在CAP附近，随着驱动力F的增加而增加，在另

剩余内容已隐藏，支付完成后下载完整资料

英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[595557]，资料为PDF文档或Word文档，PDF文档可免费转换为Word