非局域非线性介质中艾里束脱落的孤子和呼吸艾里孤子的束缚态外文翻译资料

英语原文共 5 页，剩余内容已隐藏，支付完成后下载完整资料

附录A 译文

非局域非线性介质中艾里束脱落的孤子和呼吸艾里孤子的束缚态

摘要

通过直接的数值模拟，我们研究了非局域非线性介质中艾里束脱落的空间光学孤子和艾里束的异常相互作用。数值结果表明，非局域性对从艾里光束中脱落的孤子的传播动力学有着深远的影响。结果还表明，强非局域性可以支持相反弯曲方向的艾里光束的周期性强度分布。非局域性也提供了艾里光束之间的长程引力，导致同相和异相呼吸艾里孤子形成稳定的束缚态，这些孤子在局域介质中总是排斥。

自加速艾里光束在非扩散波包[5]实验实现[4]后引起了广泛的关注[1,2,3]。艾里光束在传播动力学和全光器件的应用中具有许多独特的特性。[6-13]除了艾里光束的线性控制外[6-13]，艾里光束的非线性控制还包含了许多新的动力学特性[14-27]。特别是在非线性介质中，孤子可以由艾里光束[28-30]形成。此外，艾里光束之间的相互作用[31,32]在束缚孤子对[33,34]的产生中起着重要的作用。

然而，上述所有的工作都是在局域非线性介质中进行研究的。结果表明，强非局域介质的边界条件深刻地影响了自加速光束[35]的传播动力学。最近，推导出了艾里光束在强非局域非线性介质中传播的解析表达式，证明了艾里光束的归一化强度分布总是周期性的[36]。在光学领域中，非局域非线性是指材料在特定位置的光诱导折射率变化是由该位置某一邻域的光强决定的。这种非局域光学非线性存在于向列相液晶[37]和热介质[38]中。许多研究表明，非定域性对孤子的传播[39]有深远的影响。非局域非线性也会影响非相[38]亮孤子[40-42]和暗孤子[43-45]的相互作用。

本文用数值方法研究了非局域非线性介质中艾里束的孤子脱落和艾里束的反常相互作用。我们发现非定域性对艾里束脱落孤子的传播动力学有深远的影响。结果表明，强非局域性可以支持相反弯曲方向的艾里光束的周期性强度分布。非定域性也提供了艾里束之间的回旋引力，导致同相和非相呼吸艾里孤子形成稳定的束缚态，这些孤子在局域介质中总是排斥。

结果

非局域非线性介质中空光束中孤子脱落的动力学。我们假设艾里光束在具有自聚焦非局域三次非线性的介质中的传播。艾里光束用归一化的非局域非线性薛定谔方程来描述，

(1)

其中，对应于归一化的非局域响应函数。在不丧失一般性的情况下，我们考虑了所谓的高斯非局域响应函数的情况：，用特征宽度来表示非局域性的程度。它分别描述了的局域性介质和[39]的强非局域性的介质。一般来说，非局域响应函数的现实形式取决于材料的潜在物理过程[47]。研究表明，只要响应函数是单调衰减的，孤子在非局域介质中的物理性质并不强烈地依赖于非局域响应函数的形状[48]。虽然高斯非局域响应函数是现象学的，但它可以描述其他实际非局域介质的一般性质[47]。

首先，通过考虑指数衰减变化[6]，研究了有限功率艾里光束在非局域非线性介质中的传播问题

， (2)

其中，为艾里光束的振幅，为保证无限艾里尾的包容和艾里光束的有限功率的衰减因子[6]。为简单起见，我们在本文中设置。

图1|艾里光束在非局域非线性介质中的传播动力学。非局域性的程度为：(a-c)（局域）和(d-f)。振幅为：(a)，(b)，(c,d)，(e)，和(f)。

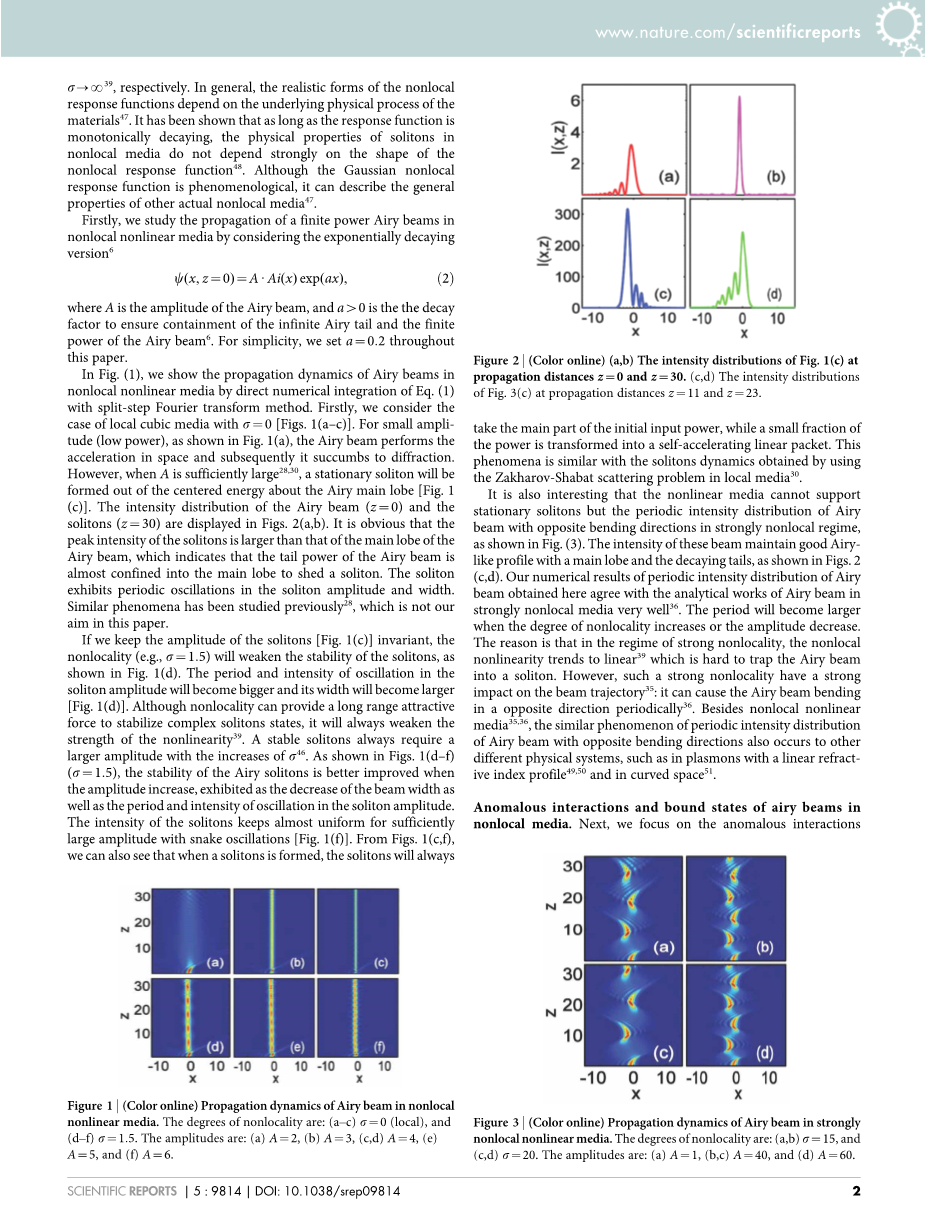
图2|(a,b)图1(c)在传播距离和处的强度分布。(c,d)图3(c)在传播距离和处的强度分布。

在图1中，我们通过等式(1)的直接数值积分展示了艾里光束在非局域非线性介质中的传播动力学与分步傅里叶变换方法。首先，我们考虑了的局域立方介质的情况。[图1(a-c)]对于小振幅（低功率），如图1(a)所示，艾里光束在空间中进行加速，随后它服从于衍射。然而，当A足够大时[28,30]，围绕艾里主叶的中心能量将形成一个静止的孤子[图1(c)]。艾里光束()和孤子()的强度分布如图2(a,b)所示。很明显，孤子的峰值强度大于艾里束的主峰的峰值强度，说明艾里束的尾功率几乎被限制在主峰中以脱落孤子。孤子在孤子的振幅和宽度上表现出周期性的振荡。类似的现象以前也被研究过[28]，这不是我们本文的目的。

如果我们保持孤子的振幅不变[图1(c)]，则非局域性(例如)将削弱孤子的稳定性，如图1(d)所示。孤子振幅的振荡周期和振荡强度会变大，振荡宽度会变大[图1(d)]。虽然非局域性可以提供一个长期的引力来稳定复杂的孤子态，但它总是会削弱非线性的强度[39]。随着[46]的增加，一个稳定的孤子总是需要一个更大的振幅。如图1(d-f)所示()，当振幅增加时，艾里孤子的稳定性得到了更好的提高，表现为光束宽度的减小以及孤子振幅的振荡周期和强度的减小。在蛇形振荡的振幅下，孤子的强度几乎保持一致[图1(f)]。从图1(c,f)中，我们也可以看到，当一个孤子形成时，孤子将总是取初始输入功率的主要部分，将一小部分功率转化为自加速线性包。这一现象与在局域介质中利用扎哈罗夫-沙巴特散射问题得到的孤子动力学[30]相似。

图3|艾里光束在强非局域非线性介质中的传播动力学。非局域性的程度为：(a,b)和(c,d)。振幅为：(a)，(b,c)和(d)。

有趣的是，非线性介质不能支持静止孤子，但可以支持在强非局域区域内弯曲方向相反的艾里光束的周期性强度分布，如图3所示。这些光束的强度保持了良好的空气状轮廓，有一个主叶和衰减的尾部，如图2(c,d)所示。本文得到的艾里束周期性强度分布的数值结果与艾里束在强非局域介质中的分析工作非常吻合[36]。当非局域性程度增加或振幅减小时，周期越大。原因是在强非局域性状态下，非局域非线性趋向于线性[39]，这很难将艾里光束捕获到孤子中。然而，这种强的非局域性对束轨迹有强烈的影响[35]：它可以导致艾里束周期性地向相反方向弯曲。除了非局域非线性介质[35,36]外，弯曲方向相反的艾里光束的周期性强度分布现象也发生在其他不同的物理系统中，如具有线性折射率轮廓的等离子体[49,50]和弯曲空间[51]。

非局域介质中通风光束的异常相互作用和束缚态。接下来，我们将重点关注异常的相互作用和非局域非线性介质中艾里光束的束缚态。我们假设入射光束由两个移位的反向传播艾里光束组成，它们之间有一个相对相位，

， (3)

其中，为控制相移的参数，为控制光束分离的参数。在本报告中，我们分别考虑了具有和的同相和异相艾里光束[33,34]。

图4|非相()艾里光束在非局域非线性介质中的相互作用。非局域性的程度为：(a-c)（局域介质）和(d-f)。所有图的振幅均为。光束分离值为：(a,d)，(b,e)和(c,f)。

同相空孤子的束缚态。在图4中，我们展示了在一些不同的光束分离下的同相艾里光束()之间的相互作用。为了进行比较，我们还用[33,34]在局域介质()中重做了一些以前的结果。对于较大的分离，两个艾里分量形成两个平行的孤子[33,34]，而对于较小的分离，束缚的呼吸孤子是以一定的周期形成的[图4(a-c)]。分离度越小，吸引力就越强，孤子呼吸的周期也就越小。当与形成的孤子周期最小时，吸引力最大[图4(a)][34]。用相同的振幅，如图4(d-f)所示的非局域非线性介质中的艾里光束与的相互作用。相互作用的动力学关键取决于艾里光束的分离：分离较大时，艾里光束的相互作用明显增强[图4(f)]，表现为周期和宽度的减小，而分离较小时，相互作用随着束缚呼吸孤子的周期和宽度的增加而减弱[图4(d)]。非定域性提供了一个长程引力，可以增强孤子之间的相互作用[52]。对于较大的艾里梁，情况是如此[图4(f)]。对于较小的分离的同相艾里光束，它们之间的吸引力足够大，可以形成只有局域非线性的束缚态[图4(a)]。然而，非定域性总是会削弱较小的分离同相艾里光束的相互作用[图4(d)]，因为非局域性会削弱非线性的强度[39]。

图5|非相()艾里光束在非局域非线性介质中的相互作用。非局域性的程度为：(a-c)（局域介质）和(d-f)。所有图的振幅均为。光束分离值为：(a,d)，(b,e)和(c,f)。

与图4(a-c)中相比，在局域介质中增加振幅到，相互作用明显减弱。[图5(a,b)]，除了较大的分离光束[图5(c)]。特别是的情况下出现了斥力，如图5(a)所示[34]。即使是由很小程度的非局域性引起的引力，也能平衡斥力。我们在图5(d)中展示了呼吸孤子的束缚态和弱非局域性的。其他分离的光束之间的相互作用也得到了增强。[图5(e,f)].

图6|非相()艾里光束在非局域非线性介质中的相互作用。非局域性的程度为：(a-c)（局域介质）和(d-f)。所有图的振幅均为。光束分离值为：(a,d)、(b,e)和(c,f)。

非相艾里光束的束缚态。对于非相艾里光束()，在局域介质和非局域介质中的相互作用分别如图6(a-c)和图6(d-f)所示。从图6(a-c)，我们可以看到孤子对实际上是由入射相互排斥而形成的[34]。时间间隔越小，排斥力就越强。孤子对的最强排斥力发生在的情况下[图6(a)][34]。对于给定的振幅，图6(d-f)清楚地表明，由于非局域性()不能平衡失相光束的排斥力，尽管分离或大或小，但非局域性会减弱相互作用。

当强自聚焦效应平衡失相斥力时，在局域介质中可以得到振幅较大的非相艾里光束的静止束缚态，如图7(a-c)所示。我们考虑了的强排斥情况。从图7(a-c)，我们可以发现分离度较小的艾里光束总是需要较大的振幅才能形成稳定的孤子对，例如，换[图7(a)]。有趣的是，我们甚至可以在小分离的下得到两个强度不同的孤子对[图7(a)]。孤子对不能从振幅较大的同相艾里束中获得，因为强的自聚焦和同相引力总是会破坏光束，导致艾里束坍塌。

图7|非相()艾里光束在非局域非线性介质中的相互作用。非局域性的程度为：(a-c)（局域介质）、(d)、(e)、(f)。图7(a-c)的振幅分别为和图7(d-f)的振幅分别为。光束分离值为：(a,d)，(b,e)和(c,f)。

在局域介质中获得的孤子对[图7(a-c)]具有较大的振幅，可能由于具有较强的自聚焦效应而变得不稳定[34]。经过一些传播距离后，例如，换，斥力将超过引力，孤子对将向相反的方向飞走[34]。利用非定域性，可以得到完全稳定的非相艾里光束束缚态，如图7(d-f)所示。振幅也应该大于局域介质的振幅[图7(a-c)]。对于这种稳定的孤子对，较小的分离度()总是需要较大程度的非局域性和振幅[图7(d)]。事实上，呼吸孤子对的稳定束缚态是非局域效应、非线性效应、衍射效应和排斥力效应之间平衡的结果。非定域性提供了一个长期引力来平衡非相艾里光束的排斥，导致束缚态的形成，而束缚态在局域介质中总是排斥。

讨论

孤子最重要和最有趣的动力学之一是它们的类粒子相互作用[53]。在纯局域非线性介质中，明亮的孤子可能会吸引、排斥，甚至形成束缚态，这取决于它们的相对相位[54]，而暗孤子的相互作用总是排斥的[55]。近年来，人们研究了在具有空间非局域非线性的介质中孤子的相互作用。非局域非线性提供了一个长程引力，导致失相亮孤子[40-42]和暗孤子[43-45]形成稳定的束缚态。这种长程非局域非线性也允许人们在实验中观察到由多极孤子组成的失相亮点阵列[56]。

到目前为止，艾里光束的相互作用动力学仅在局域介质中进行了研究[31-34]。对于非相的艾里光束，它们在局域介质中总是被排斥[33,34]。当同相艾里光束的振幅（能量）足够大时[34]，这种排斥力也存在于它们中。因此，自然就出现了一个问题：人们能在非线性介质中获得艾里光束的稳定束缚态（孤子对）吗？

图8|非局域非线性介质中5%随机噪声扰动下的非相()艾里光束的演化。非局域性的程度是：(a)，和(b)。图8(a,b)中的振幅分别为。光束分离值分别为：(a)和(b)。

在本报告中，在非局域性的帮助下，我们得到了非局域非线性介质中同相和非相艾里光束的束缚态（孤子对）。我们还用数值方法检验了束缚态的稳定性。利用5%的随机噪声扰动对初始艾里光束进行扰动，然后对其演化进行数值模拟。如图8所示，我们只考虑非相艾里光束的情况。我们可以看到，呼吸艾里孤子的束缚态肯定是稳定的，并且在扰动下稳定地传播。综上所述，非定域性为艾里光束提供了一个长程引力，从而形成了呼吸艾里孤子的稳定束缚态，该束缚态在局域介质中总是相互排斥的。

方法

分步傅里叶变换方法。在对艾里光束传播动力学及其相互作用的数值模拟中，采用分步傅里叶变换形方法对非线性薛定谔方程(1)进行积分。该方法依赖于小步计算解，并分别处理线性步骤和非线性步骤[57]。首先，我们重写了等式(1)为：

， (4)

其中和是线性和非线性算子，

， (5)

， (6)

各自地。对于在传播距离处的光束，在下一步中，可以用分步法得到光场分布。在步骤的前半部分，我们只考虑线性算子的影响

， (7)

然后考虑整步中的非线性算子

， (8)

最后，在步骤的后半部分，再次考虑线性算子，得到光场分布为

。 (9)

非局域卷

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[587410]，资料为PDF文档或Word文档，PDF文档可免费转换为Word